——列方程解决问题的优越性

近段时间我们四年级学生在学习列方程解决应用题。但大部分孩子不能理解为什么要学习方程解决应用题,他们还是习惯用算数方法解决。后来我发现因为现在他们所面对的应用题都是比较简单的应用题。用方程解决，步骤比较麻烦，所以孩子们不太喜欢。

所以本节课我故意设计了一套对比练习，让学生从中体会用方程解决问题的优越性。题目如下：

王叔叔驾车从王村到李村办事，去时以每小时40千米的速度，行驶了3小时。沿原路返回时行驶2小时，返回时王叔叔驾车平均每小时行驶多少千米？

师：你能找到题中的相等关系吗？

生：我找到了两个相等关系。去时的速度x去时的时间=去时的路程；返回的速度x返回的时间=返回的路程

生：我还发现一个相等关系:去时的路程=返回的路程。

我根据学生的回答逐个板书上面的三个相等关系式，并追问你能够把上面的这三个相等关系式变成一个相等关系式吗？

生:去时的速度x去时的时间=返回时的速度x返回时的时间。

师：重新组成的等量关系中，你能够找到哪些是已知的量，哪个是要求的问题吗？请选择合适的方法进行解答。

这是整合了算术法解决问题与列方程解决问题的思路之后，形成的分析相等关系的一种解题思路。既适合于算术方法解决问题时梳理出思路图，也适用于列方程解决问题时寻找相等关系。

显然，从上面的相等关系可以看出补充的问题适合于列方程解决。但是，由于受算术思维的长期影响。在这一练习题的独立尝试时，有一部分学生还是习惯于用算术方法解答。这时，我把这一问题，改编如下:

王叔叔驾车从王村到李村办事。去时以每小时40千米的速度行驶了3小时。返回已经行驶了2小时，但还差10千米，返回时王叔叔驾车平均每小时行驶多少千米？

我请学生按上面的要求进行分析，通过对相等关系的分析组合，形成如下新的相等关系:

返回的速度x返回已经行驶的时间+10=去时的速度x去时的时间。

学生根据相等关系式列式解答。反馈后，教师把题目中的信息与问题罗列如下：

(1)去时速度40千米/时 

(2)去时用时3小时  

(3)返回速度55千米/时

(4)返回已经行驶了2小时

(5)距离李村还有10千米

要求学生选择其中一个信息作为问题，组合成新的应用问题并分别列出算式与方程。为提高效率，小组合作完成，并以小组为单位进行汇报，教师进行整理。

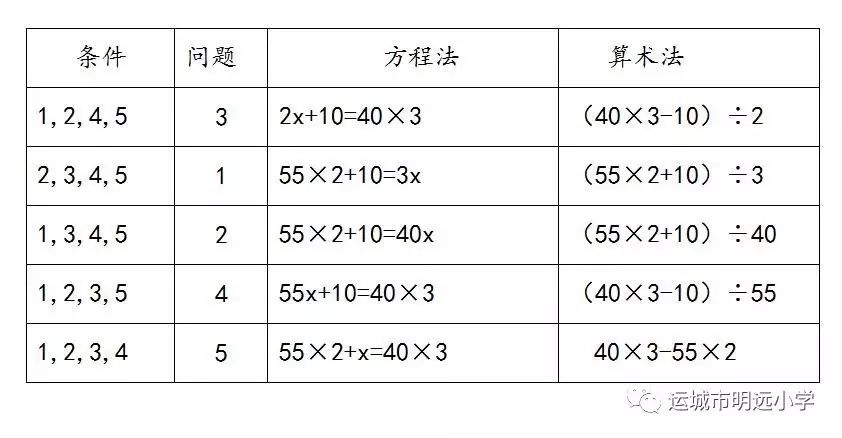
从表格中,学生直观的感受到,列方程解决问题时可以不改变原来的相等关系,“以不变应万变”列出不同的方程。

把列方程解决问题的思路纳入一般的应用问题的分析思路之中，让学生通过分析、辨析与判断，在解决应用题的一般思路下逐步总结出列方程解决问题的思考步骤，体会到列方程解决问题的优越性。